If you had to pick a few words or symbols to sum up your legacy, what would you choose? Johann Carl Friedrich Gauss (1777–1855) left behind a trophy case full of mathematical achievements to choose from, but above all, he wanted a “regular heptadecagon” engraved on his tombstone. The highly symmetrical, 17-sided shape was evidence of what Gauss considered one of his greatest contributions to mathematics. At just 18 years old, Gauss used a heptadecagon to solve a classic problem that mathematicians had been wrestling with for more than 2,000 years. A tour through that history reveals deep connections between the ancient concept of shapes as drawings and a modern perspective on the equations that govern them.
Ancient Greek Geometry
The ancient Greeks excelled in geometry, placing particular emphasis on constructions involving a compass and ruler. Consider these constructions as diagrams with desired geometric properties made using only one writing utensil and two tools. Given two points, a compass (not to be confused with the navigation device) draws a circle centered at either point and passing through the other point. A ruler draws straight lines between points. Neither tool has markings, so they cannot measure distances or angles.
About supporting science journalism
If you like this article, please consider supporting our award-winning journalism by Subscribe. By purchasing a subscription, you help secure a future of impactful stories about the discoveries and ideas shaping our world today.
The Greeks did not impose arbitrary rules just to make mathematics more challenging. The game of constructing shapes with a compass and straightedge has its origins in Euclid’s Elements, one of the most important textbooks ever written. Like modern mathematicians, Euclid wanted to derive all of geometry from a minimal list of assumptions, called postulates. Rather than simply asserting the existence of shapes or other geometric objects, Euclid wanted to explicitly build them from their simplest ingredients: lines and circles.
To get a feel for these constructions, try one yourself. Given the line segment of A Unpleasant B below, find the center. Looking is not enough; your method must find the exact center.

First use the compass to draw a circle with the center A and passing by B (first panel). Then repeat this step with the circle in the middle B and passing by A (second panel). These circles intersect at two points. Use the ruler to connect these points (third panel). Due to the symmetry in our construction, this vertical line will intersect the original line segment exactly in the middle.
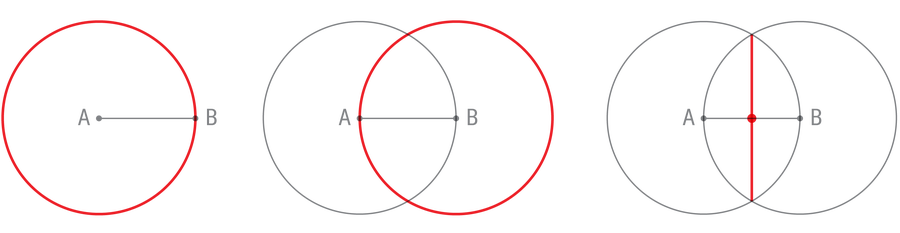
This construction does much more than bisect a line segment. It creates a right angle between the two lines, which is no easy task with such a limited tool set. And by connecting a few more points, you can create an equilateral triangle, a triangle whose sides are equal in length (and whose angles are equal in size).
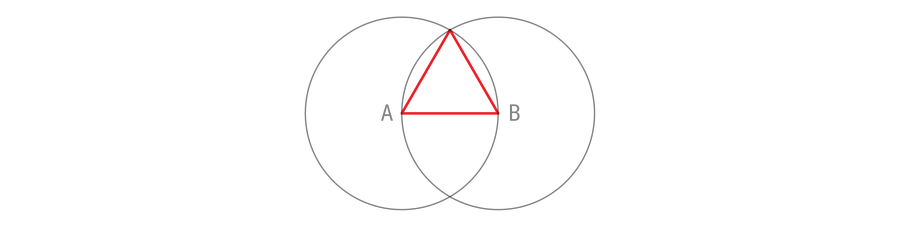
Note that each edge of the triangle is also a radius of one of the circles. The circles are the same size and therefore all sides of the triangle have the same length. Equilateral triangles are therefore constructible with a compass and straightedge, QED. Congratulations on maintaining the first proposition in the first book of Euclid ElementsOnly 13 more books to go.
An obstacle
Of all the shapes you can construct with a compass and ruler, regular polygons have a special cachet. Polygons are closed shapes consisting of straight edges, such as triangles and rectangles (as opposed to curved shapes such as circles or non-closed shapes such as the letter E). Normal Polygons have the most symmetry, because their sides are all the same length and their angles are all the same size (like squares and equilateral triangles, but unlike rectangles and rhombuses). Constructing any irregular triangle with a compass and straightedge is a breeze: just scatter three points on the page and connect them with lines. But constructing our perfectly symmetrical equilateral triangle, a regular polygon, required some elegant legwork.
Euclid discovered how to construct regular polygons with three, four, and five sides, or equilateral triangles, squares, and regular pentagons, respectively. He squeezed a few more generalizations out of these core constructions; for example, once you have a regular polygon on the page, a simple maneuver will produce a new regular polygon with twice the number of sides.
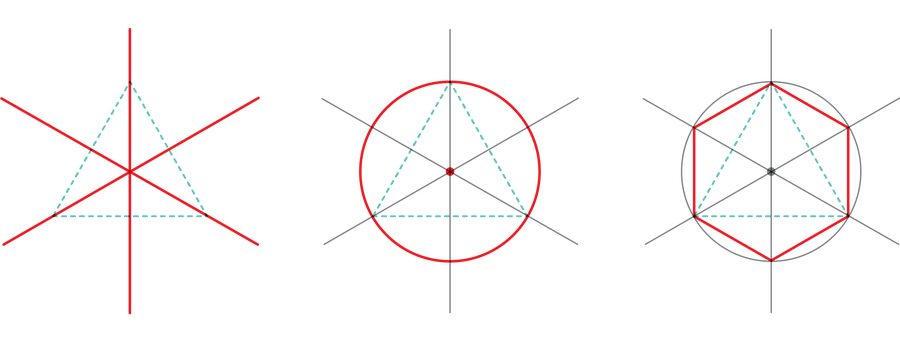
You can repeat this doubling procedure as many times as you like. That means that three-, four-, and five-sided regular polygons can be transformed into six-, eight-, and ten-sided regular polygons, as well as 12-, 16-, and 20-sided ones, and so on. Euclid also showed how to “multiply” the three- and five-sided regular polygons to produce a regular 15-sided polygon.
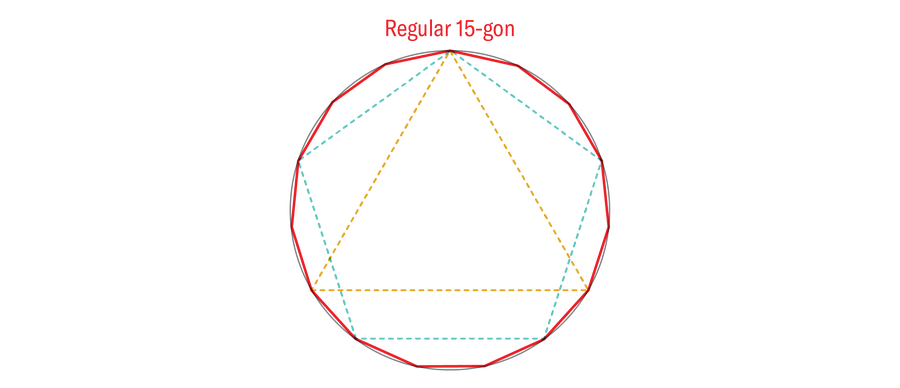
Progress stalled there. Somehow, Euclid knew that a regular 3,072-sided triangle was in principle constructible (a triangle doubled 10 times), but he had no idea how to construct a regular heptagon or hendecagon. To be clear, regular polygons with a side count greater than two do exist and can be constructed with more capable tools. The question Euclid left was which ones were constructible with only a compass and straightedge. This question would remain unanswered for two millennia until a certain German teenager picked up a pencil.
18th century mathematics provides a solution
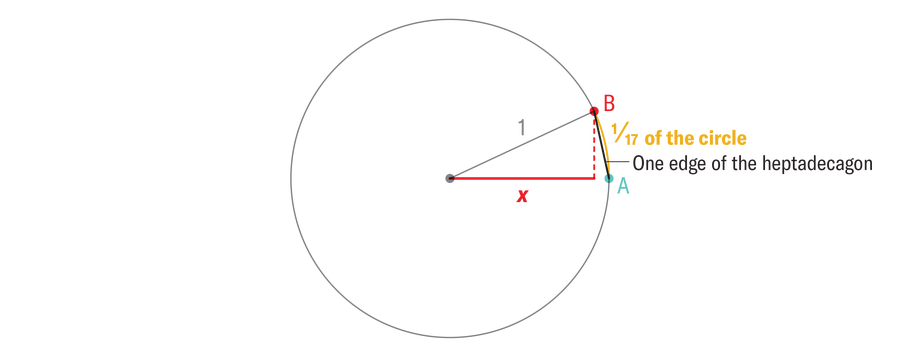
In 1796, no new regular polygons had been added to the pantheon of constructible shapes, but mathematicians had gained a deeper understanding of compass and straightedge constructions. Gauss knew how to reduce the problem of constructing a regular polygon to constructing a line segment of a very specific length. To see how to construct a 17-sided polygon, start with a unit circle (with a radius of one) and a point A on the circle. Imagine if we could find the red point B above A exactly one seventeenth of the circle. If we could construct the red point from the blue point, we could repeat that construction all the way around the circle, connect the points with our ruler, and voilà, a regular heptadecagon. How to draw point B, given point A, although? Note that if we take the red line segment labeled X, then we can trace that to the red dot B, and we win. The whole problem of constructing a regular heptadecagon comes down to constructing a line segment of precise length XFor the mathematically curious, X = cosine (2π ⁄17).
Can a straightedge and compass construct a line segment of any length? In Gauss’s day, mathematicians knew the surprising answer to this question. A length is constructible if it can be expressed by the operations of addition, subtraction, multiplication, division, or square roots applied to integers. Thus, some strange numbers such as the square root of 99⁄5 are constructible (99 and 5 are integers, and we have applied division and square root to them), while some more familiar numbers such as pi (π) and the cube root of 2 cannot be constructed, because you can never write them in terms of just these five operations.
Remarkably, the rudimentary tools that the ancient Greeks used to draw their geometric diagrams correspond perfectly to the natural operations of modern algebra: addition (+), subtraction (–), multiplication (x), division (/), and square roots (√). The reason for this is that the comparisons for lines and circles only these five operations are used, a perspective that Euclid could not have imagined in the pre-algebra era.
You may be surprised to know that Gauss never actually drew a regular heptadecagon. He didn’t need to. He proved that the shape is in principle constructible by expressing the special length X [cosine (2π ⁄17)] only in terms of the five algebraic operations that the compass and straightedge allow. Even if you don’t find his equation particularly illuminating, its complexity shows how much work the adolescent must have put into the problem:

Even more impressively, Gauss fully characterized which regular polygons are constructible and which are not (although it was not until 1837 that Pierre Wantzel provided a rigorous proof that Gauss’s characterization left nothing out). Thus, not only did Gauss describe the shape that all constructible regular polygons take, he and Wantzel vindicated Euclid’s frustrations by proving that the elusive regular heptagon (seven sides) and the hendecagon (eleven sides) impossible to construct using only a compass and ruler, along with an infinite number of other shapes.
According to biographer G. Waldo Dunnington, Gauss felt very proud of solving the age-old problem and told a friend that he wanted a regular heptadecagon on his gravestone. Unfortunately, that didn’t happen, but a monument in Gauss’s hometown of Brunswick, Germany, has a 17-pointed star engraved on the back. The stonemason chose a star because he believed that humans would not be able to distinguish a heptadecagon from a circle. I wonder if Euclid would agree.



